Keywords: Neural Network Architecture, Modular Neural Network, Simulation, Generalization, Neural Networks

This paper focuses on the powerful concept of modularity. It is descried how this concept is deployed in natural neural networks on an architectural as well as on a functional level.

Furthermore different approaches for modular neural networks are discussed.

Based on this a two layer modular neural system is introduced. The basic building blocks of the architecture are multilayer Perceptrons (MLP) trained with the Backpropagation algorithm.

This modular network is designed to combine two different approaches of generalization known from connectionist and logical neural networks; this enhances the generalization abilities of the network.

Experiments described in this paper show that the architecture is especially useful in solving problems with a large number of input attributes.

Modularity is a very important concept in nature. Modularity can be defined as subdivision of a complex object into simpler objects. The subdivision is determined either by the structure or function of the object and its subparts.

Modularity can be found everywhere; in living creatures as well as in inanimate objects. The subdivision in less complex objects is often not obvious.

At a very basic level electrons, positrons, and neutrons make the building blocks for any matter. At a higher level, atoms of elements are another form of simple modules of which everything is constructed. In living creatures proteins and on a higher level, cells could be seen as basic components. This idea of modules can be continued to more and more complex structures. Even looking at the universe planets can be seen as modules within a solar system.

Replication and decomposition are the two main concepts for modularity. These concepts are found in concrete objects as well as in thinking. It is often difficult to discriminate sharply between them; replication and decomposition often occur in combination.

Replication is a way of reusing knowledge. Once one module is developed and has proved to be useful it is replicated in a larger number. This principle is often found in living organisms. Observing a human this can be seen in a various scale: two similar legs, fingers, vertebra of similar structure, thousands of hair modules, and billions of cells. In electronics, the development of integrated circuits is based on replication of simple units to build a complex structure.

Decomposition is often found when dealing with a complex task. It is a sign of intelligent behavior to solve a complex problem by decomposing it into simpler tasks which are easier to manage and then reassemble the solution from the results of the subtasks. Constructing large software, building a car, or solving an equation are usually done by decomposing the problem.

The nervous system anatomic structures underline the modular characteristics of the human brain on several levels. The connections and the structure of the modules and their interaction result in intelligent behavior [2], [9].

A modern research method to locate functional units of the brain is to use Positron-emission tomography (PET). The test subject receives an injection of glucose with a radioactive label (with a very short half-live ranging).

The regions that are more active need more energy; the concentration of glucose and therefore the concentration of the radioactive label will be higher in these parts than in other parts of the brain. Using PET these regions can be localized. It is assumed that the region that is most active, is the part of the central nervous system (CNS) that deals with the task. For a more comprehensive description see [16].

One cognitive task can involve different processes. Most tasks involve a combination of serial and parallel processing.

It can be observed that while humans have the ability to do different things in parallel; some parallel tasks are easier than others. Most people have no problems with walking and talking in parallel; whereas they find listening to two different speakers at the same time very difficult. This implies that tasks that can be processed in different modules can be done easily in parallel, whereas tasks that need the same processing unit are difficult to manage concurrently.

Neuropsychologists study the information processing system of humans. They focus especially on patients with a partly damaged brain. The damage of a region of the brain has implications on the cognitive abilities which are situated in this area. The non-damaged parts are still working; in some cases their performance is improved to compensate the loss in the other parts.

This observation suggests that the brain has a highly modular and parallel structure [5].

The most used artificial neural networks have a monolithic structure. These networks perform well on a very small input space. However, the complexity increases and the performance decreases rapidly with a growing input dimension [12].

A lot of research is being done to overcome these problems; many of the ideas include modularity as a basic concept.

But the main problem remains how to chose modules, how to structure the problem? One approach is to use human design knowledge to restructure the problem and the data set for the modular solution. This approach is only applicable for a very limited domain of problems.

Another way is to use modular neural systems. In [14] a locally connected adaptive modular neural network is described. This model employs a combination of BP training and a Winner-Take-All layer.

A modular neural system using a self-organizing map and a multilayer Perceptron is presented in [6]. It is applied in a cosmic ray space experiment.

Many other researchers have also investigated the concept of modularity and the impact on neural networks [3], [4], [6], [7], [8], [10], [11], [13], and [14].

In the following section a modular neural network is proposed to enhance the generalization ability of neural networks for high dimensional inputs. The network consists of several MLPs. Each of the modules is trained by the BP algorithm. The number of weight-connections in the proposed architecture is significantly smaller than in a comparable monolithic network.

Inspired by the ideas of modularity and dismissing the concept of a perfect and general neural system a new modular neural network architecture is proposed.

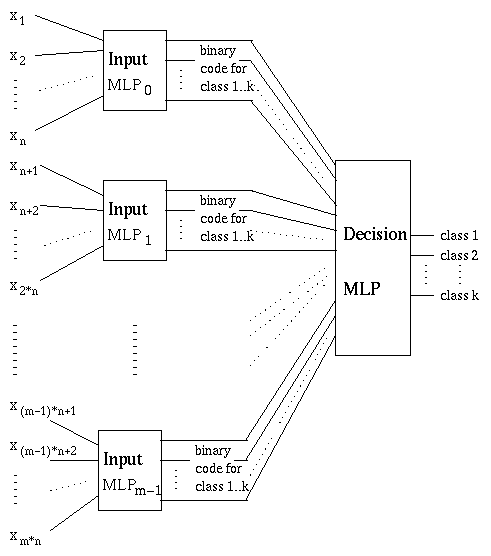
One prototype of this architecture is a two-layer modular neural system [17]. In this prototype each module is a multilayer Perceptron. Each input variable is connected to only one of the input modules. These connections are chosen at random. The outputs of all input modules are connected to the decision network. The structure is depicted in Figure 1.

Figure 1: The Modular Neural Network Architecture

The supervised training occurs in two stages. All the modules are trained using the Backpropagation algorithm.

In the first phase all sub-networks in the input layer are trained. The training set for each sub-network is selected from the original training set. The training pair for a single module consists of the components of the original vector, which are connected to this particular network (as input vector) together with the desired output class represented in binary coding.

All input modules can be trained in parallel very easily because they are all mutually independent.

In the second stage the decision network is trained. The training set for the decision module is built from the output of the input layer together with the original class number. To calculate the set each original input pattern is applied to the input layer; the resulting vector together with the desired output class (represented in a 1-out-of-k coding) form the training pair for the decision module.

The training algorithm is described in more detail in [17].

The output calculation for new input vectors is also performed in two stages. First the new input vector is presented to the input modules. Then the outputs of the input modules are used as input for the decision module. On the basis of this input the final result is calculated. The k-dimensional output of the decision module is used to determine the class number for the given input.

The ability to generalize is the main property of neural networks. This is how neural networks can handle inputs which have not been learned but which are similar to inputs seen during the training phase. Generalization can be seen as a way of reasoning from a number of examples to the general case. This kind of reasoning is not valid in a logical context but can be observed in human behavior.

The proposed architecture combines two methods of generalization.

One way of generalizing is built-in to the MLP. Each of the networks has the ability to generalize on its input space. This type of generalization is common to connectionist systems.

The other method of generalization is due to the architecture of the proposed network. It is a way of generalizing according to the similarity of input patterns. This method of generalization is found in logical neural networks [1, p172ff,].

The proposed architecture was implemented in C++ and simulations with different real-world data sets were carried out and compared to MLPs.

The proposed architecture was tested with different real-world data sets. The number of input attributes was between eight and 12000.

Throughout the experiment it appeared that the modular network converged for a large range of network parameters. Particularly for huge input spaces it was often very difficult to find an appropriate learning coefficient for a monolithic network, whereas convergence was no problem for the modular structure.

The time needed to train the modular network was much shorter than that for a monolithic network. In most cases it took less than half the time to train the network to a similar performance. For larger input spaces the training was up to ten times quicker (without parallel training).

For small input spaces (up to 60 attributes) the memorization and generalization performance of the modular network and a monolithic MLP were very similar on the real-world data sets.

As an example for large input spaces a comparison was made on the ability to recognize noisy inputs. The task was to memorize five pictures of different faces. Each gray-level pictures had a size of 75 by 90 pixels (6750 continuous inputs). The original pictures are from [18].

Figure 2: Examples of Noisy Test Pictures

After training the generalization performance was tested with noisy pictures. The noise on the pictures was generated randomly. In Figure 2 pictures with different noise-levels are shown. The modular network could recognize pictures with a significant higher noise-level than the single MLP; the results are shown in Figure 3.

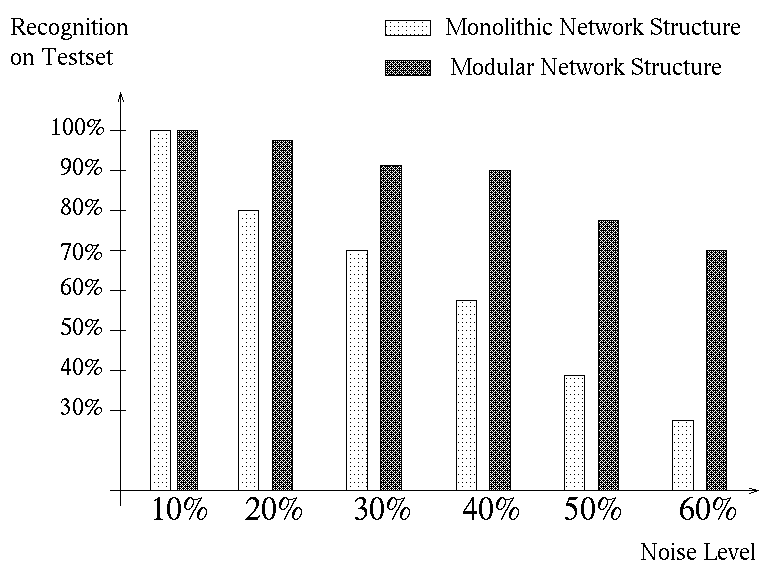
Figure 3: The Performance on Noisy Inputs

From the above experiments it can be seen that the modular network has superior generalization abilities on high dimensional input vectors.

The proposed architecture has certain theoretical limitations on statistically neutral problems. Monolithic MLPs are able to learn such problems but the generalization performance is very poor [15].

Inspired by nature the usage of modular and only partially connected neural networks is proposed.

Two different approaches of generalization are combined in this model which results in a better generalization performance.

Experiments with a modular architecture are demonstrated. This way of building larger networks seems to be very promising.

It is shown that for different real world data sets the training is much easier and faster with a modular architecture. Due to the independence of the modules in the input layer parallel training is readily feasible.

Statistically neutral problems can not be tackled with this neural network architecture.

[6] R. BELLOTTI, M. CASTELLANO, C. DE MARZO, G. SATALINO. Signal/Background classification in a cosmic ray space experiment by a modular neural system. In: Proc. of the SPIE - The International Society for Optical Engineering. Vol: 2492, Iss: pt.2, Page 1153-61. 1995.