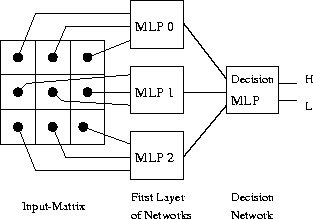
Figure 2: The Example Architecture.
The ability to generalize is the main property of neural networks. This is how neural networks can handle inputs which have not been learned but which are similar to inputs seen during the training phase. Generalization can be seen as a way of reasoning from a number of examples to the general case. This kind of reasoning is not valid in a logical context but can be observed in human behaviour.
The proposed architecture combines two methods of generalization.
One way of generalizing is built-in to the MLP. Each of the networks has the ability to generalize on its input space. This type of generalization is common to connectionist systems.
The other method of generalization is due to the architecture of the proposed network. It is a way of generalizing according to the similarity of input patterns. This method of generalization is found in logical neural networks [1, p172ff,].
To explain the behaviour more concretely the following simplified example of a recognition system is given.

Figure 2: The Example Architecture.
A 3x3 input retina with the architecture shown in Figure 2 is assumed. Each of the nine inputs reads a continuous value between zero and one, according to the recorded gray level (black=1; white=0).
The network should be trained to recognize the simplified letters 'H' and 'L'. The training set is shown in Figure 3. The desired output of the input networks is '0' for the letter 'H' and '1' for the letter 'L'.
The training subsets for the networks MLP![]() , MLP
, MLP![]() , and
MLP
, and
MLP![]() are:
are:
|
MLP | MLP | MLP |
| (1,0,1;0) | (1,1,1;0) | (1,0,1;0) |
| (1,0,0;1) | (1,0,0;1) | (1,1,1;1) |
After completing the training of the first layer of networks it is assumed
that the calculated output is equivalent to the desired output.The
resulting training set for the decision network is:
![]()
![]()
After the training of the decision network the assumed response of the
system to the training set is:
![]()
![]()
To show the different effects of generalization three distorted characters, shown in Figure 4 are used as the test set:
The first character tests generalization within the input modules, the second shows the generalization on the number of correct sub-patterns, and the third character is an example of a combination of both. (The figures in the input vectors are according to the gray-level in the pattern; the outputs are taken from a typical neural network).
![]()
![]()
![]()